arctanx的导数是什么（arctanx多次求导）

6. 函数单调性：

注①： 若点x0是可导函数f(x)极值点，则f&39;(x)=0. 但反过来不一定成立. 对于可导函数，其一点x0是极值点的必要条件是若函数在该点可导，则导数值为零.

II. (ln x)&39;=1/x (log a x)&39;=1/xlogae (arctanx)&39;=1/(x2+1)

注：①可导的奇函数函数其导函数为偶函数.

也就是说x0是极值点的充分条件是x0点两侧导数异号，而不是f&39;(x)=0①. 此外，函数不可导的点也可能是函数的极值点②. 当然，极值是一个局部概念，极值点的大小关系是不确定的，即有可能极大值比极小值小（函数在某一点附近的点不同）.

例如：函数y=f(x)=x3，x=0使f&39;(x)=0，但x=0不是极值点.

①如果在x0附近的左侧f&39;(x)＞0，右侧f&39;(x)＜0，那么f(x0)是极大值；

事实上，令x=x0+?x,则x→x0相当于?x→0.

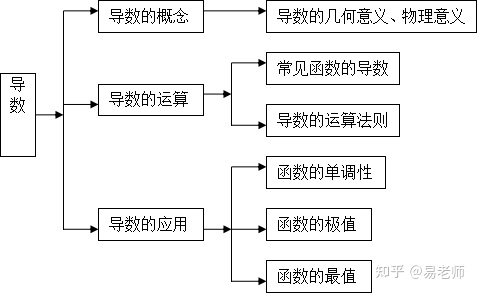
I.C&39;=0（C为常数） (sinx)&39;=cosx (arcsinx)&39;=1/√(1-x2)

可以证明，如果y=f(x)在点x0处可导，那么y=f(x)点x0处连续.

于是

函数y=f(x)在点x0处的导数的几何意义就是曲线y=f(x)在点(x0,f(x))处的切线的斜率，也就是说，曲线y=f(x)在点P(x0,f(x))处的切线的斜率是f&39;(x0)，切线方程为y-y0=f&39;(x)(x-x0).

7. 极值的判别方法：（极值是在x0附近所有的点，都有f(x)＜f(x0)，则f(x0)是函数f(x)的极大值，极小值同理）

存在，则称函数y=f(x)在点x0处可导，并把这个极限叫做y=f(x)在x0处的导数，记作f′(x0)或y′|x=x0，即f′(x0)=

注：①?x是增量，我们也称为“改变量”，因为?x可正，可负，但不为零.

⑵常数的判定方法；

②以知函数y=f(x)定义域为A，y=f&39;(x)的定义域为B，则A与B关系为包含且等于.

注：①f(x)>0是f（x）递增的充分条件，但不是必要条件，如y=2x3在(-∞,+∞)上并不是都有f(x)>0，有一个点例外即x=0时f（x） = 0，同样f(x)<0是f（x）递减的充分非必要条件.

3. 导数的几何意义：

②形如y=(x-a?)(x-a?)...(x-an)或y=(x-a?)(x-a?)...(x-an)/(x-b?)(x-b?)...(x-bn)两边同取自然对数，可转化求代数和形式.

⑴函数单调性的判定方法：设函数y=f(x)在某个区间内可导，如果f&39;(x)＞0，则y=f(x)为增函数；如果f&39;(x)＜0，则y=f(x)为减函数.

2. 函数y=f(x)在点x0处连续与点x0处可导的关系：

（e的x次方)&39;= e的x次方 (a的x次方)&39;=a的x次方lna (arc cotx)&39;=-1/(x2+1)

(u±v)&39;=u&39;±v&39;=>y=f?(x)+f?(x)+...+fn(x)=>y&39;=f&39;?(x)+f&39;?(x)+...+f&39;n(x)

⑵如果y=f(x)点x0处连续，那么y=f(x)在点x0处可导，是不成立的.

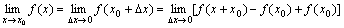
例：f(x)=|x|在点x0=0处连续，但在点x0=0处不可导，因为?y/?x=|?x|/?x，当?x＞0时，?y/?x=1；当?x＜0时，?y/?x=-1，故

(u/v)&39;=(vu&39;-v&39;u)/v2(v≠0)

③无理函数或形如y=x的x次方这类函数，如y=x的x次方取自然对数之后可变形为y=lnx，对两边求导可得y/y=lnx+x*1/x=>y&39;=ylnx+y=>y&39;=x的x次方lnx+x的x次方.

5. 复合函数的求导法则：f&39;x(φ(x))=f&39;(u)φ&39;(x)或y&39;x=y&39;u·u&39;x

如果函数y=f(x)在区间I内恒有f&39;(x)=0，则y=f(x)为常数.

注：①u,v须是可导函数.

②可导的偶函数函数其导函数为奇函数.

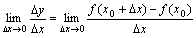
不存在.

注：函数的极值点一定有意义.

②若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导.

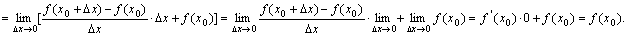
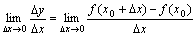
当函数f(x)在点x0处连续时，

III. 求导的常见方法：

⑴函数y=f(x)在点x0处连续是y=f(x)在点x0处可导的必要不充分条件.

8. 极值与最值的区别：极值是在局部对函数值进行比较，最值是在整体区间上对函数值进行比较.

(x?)&39;=nx(n-1)次方（n∈R） (cosx)&39;=-sinx (arccosx)&39;=-1/√(1-x2)

1. 导数（导函数的简称）的定义：设x0是函数y=f(x)定义域的一点，如果自变量x在x0有增量?x，则函数值y引起相应的增量?y=f(x0+?x)-f(x0)；比值?y/?x=[f(x0+?x)-f(x0)]/?x称为函数y=f(x)在点x0到x0+?x之间的平均变化率；如果极限

②例如：函数y=f(x)=|x|，在点x=0不可导，但点x=0是函数的极小值点.

9. 几种常见的函数导数：

4. 求导数的四则运算法则：

例如：设f(x)=2sinx+2/x，g(x)=cosx-2/x，则f(x),g(x)在x=0处均不可导，但它们和f(x)+g(x)=sinx+cosx在x=0处均可导.

更多精彩内容：「链接」

①常用结论：(ln|x|)&39;=1/x.

(uv)&39;=vu&39;+v&39;u=>(cv)&39;=c&39;v+cv&39;=cv&39;(c为常数）

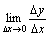
②一般地，如果f（x）在某区间内有限个点处为零，在其余各点均为正（或负），那么f（x）在该区间上仍旧是单调增加（或单调减少）的.

.

复合函数的求导法则可推广到多个中间变量的情形.

②如果在x0附近的左侧f&39;(x)＜0，右侧f&39;(x)＞0，那么f(x0)是极小值.